LEY DE ARQUIMEDES

Dadme un punto de apoyo. . .

Otra anécdota conocida de Arquímedes, según la cual éste habría pronunciado la célebre frase, tan retórica: Dadme un punto de apoyo y levantaré el mundo, está narrada por Pappus¹ y Plutarco, en conexión con el problema: mover un peso dado, mediante una fuerza dada.

Arquímedes, pariente y amigo de Hierón, le escribió que con una potencia dada se puede mover un peso igualmente dado, y jugando, como suele decirse, con la fuerza de la demostración le aseguró que si le dieran otra tierra movería ésta después de trasladarse a aquella. Maravillado Hierón y pidiéndole que verificará con obras este problema e hiciese ostensible cómo se movía alguna gran mole con una potencia pequeña, utilizó un gran transporte de tres velas del arsenal del rey, que fue sacado a tierra con mucho trabajo y a fuerza de un gran número de brazos; cargándole de gente y del peso que solía echársele, y sentado lejos de él, sin esfuerzo alguno y con solo mover la mano al cabo de una máquina de una fuerza atractiva, lo llevó así derecho y sin detenerse como si corriese por el agua. Pasmóse el rey, y convencido del poder de arte encargó a Arquímedes que le construyese toda especie de máquinas de sitio, bien fuese para defenderse, o más bien para atacar; de las cuales él no hizo uso, habiendo pasado la mayor parte de su vida exenta de guerra y en la mayor comodidad; aunque luego tuvieron los siracusanos menester de aquellas máquinas y de su artífice. (Parra, E. 2008)

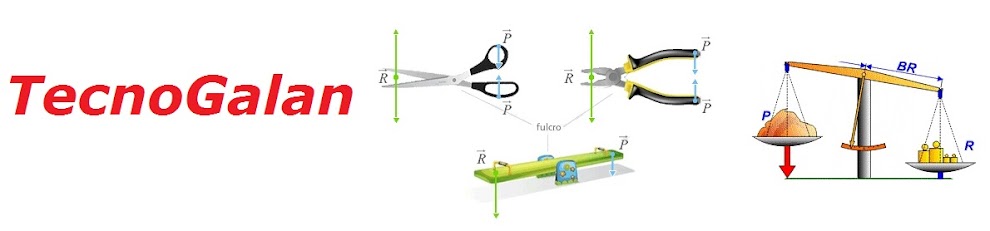
El famoso comentario de Arquímedes demuestra hasta qué punto había llegado a comprender el mecanismo del fulcro. Se trata literalmente de un soporte o puntal colocado de tal forma que permite que una fuerza comparativamente pequeña levante un peso comparativamente grande. El fulcro se puede utilizar como punto de apoyo de una palanca o, como en el caso del Siracusa, un sistema de poleas. En una de las mejores obras de Arquímedes, Del equilibrio de los planos, dedicada a las palancas, se indica cómo determinar el centro de gravedad de diversas figuras planas, es decir, bidimensionales. Como en todas sus obras, Arquímedes se ciñó al formato establecido por Euclides. Los postulados (o definiciones) van seguidos de proposiciones (o teoremas) que a continuación son demostrados, y cada demostración se deriva de la demostración anterior. Primero Arquímedes enuncia el principio fundamental de las palancas, de acuerdo al cual «dos cuerpos se equilibran a distancias recíprocamente proporcionales a sus magnitudes».

Para que los dos pesos A y B se equilibren en la figura superior:

A es a B como d es a 1.
A:B = d:1 ó A/B = d/1. (Strathern, P. 1999)

De donde se deduce que: R/F = dF/dR, ¿Por qué?

Porque:

A  =  a la Carga o Resistencia

B  =  a la Fuerza Aplicada o Potencia

d   =  a la distancia de Fuerza y

1   =  a la distancia de Resistencia.

De donde  R/F = dF/dR, es igual a :          F * dF = R * dR

Lo cual da origen al enunciado del principio fundamental de las palancas o Ley de Arquímedes que dice:

"El esfuerzo multiplicado por su distancia al punto de apoyo es igual a la carga multiplicada por su distancia al punto de apoyo".